Step 3 of 6
Equation de continuité
Comme l'équation de Bernoulli, l’équation de continuité est aussi une expression de la loi de conservation de l’énergie. Elle spécifie que le flux, produit de la surface et de la vélocité (S • V) est identique tout au long d’un parcours puisque les liquides sont incompressibles:
S1 • V1 = S2 • V2
où S et V sont les surfaces et les vélocités à deux endroits différents (Figure 25.162). Si l’on connaît S1, V1 et V2, il est possible de calculer S2:
S2 = (S1 • V1) / V2
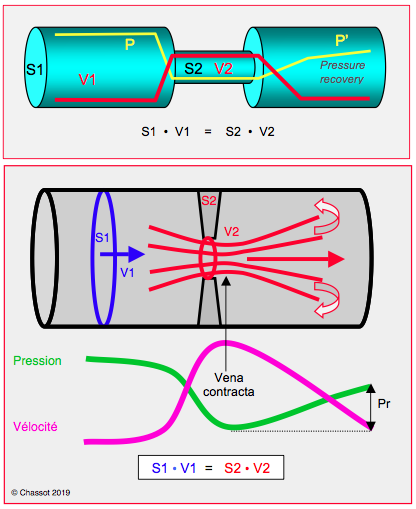
Figure 11.162 : L’équation de continuité exprime la loi de conservation de masse : le produit de la vélocité du flux (trait rouge) et de la surface du tube est constant. Dans la zone rétrécie, la vélocité augmente, mais la pression baisse (trait jaune dans le schéma supérieur, trait vert dans le schéma inférieur); c’est le principe de la conservation de l’énergie cinétique. La pression remonte dans la zone distale au rétrécissement (Pr: pressure recovery), avec une perte de charge due aux frottements et aux tourbillons (P’ < P). L’échocardiographie mesure le gradient de pression à partir de la vélocité maximale : ΔP = 4 (V22 – V12), donc au niveau de la vena contracta et avant la récupération de pression [6].
Hormis les pertes dues à la friction, le produit de l'énergie cinétique (Ec) et de l'énergie de pression (Ep) reste constant. Au passage d'une sténose, la vitesse s'accélère (hausse de Ec) et la pression diminue (baisse de Ep); c'est la situation juste à la sortie de la sténose, au niveau de la vena contacta (voir Doppler couleur). Au-delà de la sténose, la chambre de réception est large, la vitesse diminue et la pression réaugmente: c'est le phénomène de la récupération de pression (pressure recovery) ou reconversion de Ec en Ep distalement à la vena contracta. Cette transformation peut représenter une diminution de 20% du gradient de pression réel à travers une sténose aortique [1].
La Vmax représente la vélocité du flux à un instant précis de la systole ou de la diastole, mais ce flux peut être évolutif au cours du cycle cardiaque. De ce fait, l'utilisation de l'intégrale des vélocités (ITV, en cm) est préférable, car elle représente l'ensemble des vélocités par rapport au temps (durée du flux). Le produit de la surface S (en cm2) et de l'ITV (en cm) donne le volume (cm3) systolique ou diastolique. L'ITV est obtenue en dessinant à l'écran l'enveloppe du flux.
Si l’on recherche la surface d’une sténose aortique, par exemple, on peut la calculer à partir du flux dans la chambre de chasse du VG (CCVG) et de la Vmax du flux à travers la valve aortique (Ao) (Figure 25.163) [2,5]:
SAo = (SCCVG • VCCVG) / VAo
La recherche de la surface aortique est une opération fréquente en clinique. Elle comporte certaines particularités.
S1 • V1 = S2 • V2
où S et V sont les surfaces et les vélocités à deux endroits différents (Figure 25.162). Si l’on connaît S1, V1 et V2, il est possible de calculer S2:
S2 = (S1 • V1) / V2
Figure 11.162 : L’équation de continuité exprime la loi de conservation de masse : le produit de la vélocité du flux (trait rouge) et de la surface du tube est constant. Dans la zone rétrécie, la vélocité augmente, mais la pression baisse (trait jaune dans le schéma supérieur, trait vert dans le schéma inférieur); c’est le principe de la conservation de l’énergie cinétique. La pression remonte dans la zone distale au rétrécissement (Pr: pressure recovery), avec une perte de charge due aux frottements et aux tourbillons (P’ < P). L’échocardiographie mesure le gradient de pression à partir de la vélocité maximale : ΔP = 4 (V22 – V12), donc au niveau de la vena contracta et avant la récupération de pression [6].
Hormis les pertes dues à la friction, le produit de l'énergie cinétique (Ec) et de l'énergie de pression (Ep) reste constant. Au passage d'une sténose, la vitesse s'accélère (hausse de Ec) et la pression diminue (baisse de Ep); c'est la situation juste à la sortie de la sténose, au niveau de la vena contacta (voir Doppler couleur). Au-delà de la sténose, la chambre de réception est large, la vitesse diminue et la pression réaugmente: c'est le phénomène de la récupération de pression (pressure recovery) ou reconversion de Ec en Ep distalement à la vena contracta. Cette transformation peut représenter une diminution de 20% du gradient de pression réel à travers une sténose aortique [1].
La Vmax représente la vélocité du flux à un instant précis de la systole ou de la diastole, mais ce flux peut être évolutif au cours du cycle cardiaque. De ce fait, l'utilisation de l'intégrale des vélocités (ITV, en cm) est préférable, car elle représente l'ensemble des vélocités par rapport au temps (durée du flux). Le produit de la surface S (en cm2) et de l'ITV (en cm) donne le volume (cm3) systolique ou diastolique. L'ITV est obtenue en dessinant à l'écran l'enveloppe du flux.
Si l’on recherche la surface d’une sténose aortique, par exemple, on peut la calculer à partir du flux dans la chambre de chasse du VG (CCVG) et de la Vmax du flux à travers la valve aortique (Ao) (Figure 25.163) [2,5]:
SAo = (SCCVG • VCCVG) / VAo
La recherche de la surface aortique est une opération fréquente en clinique. Elle comporte certaines particularités.
- SCCVG: surface de la CCVG calculée par son diamètre mesuré en vue long axe rétrocardiaque à 120° (en moyenne 1.9-2.2 cm): S = π • r2 = 0.785 • D2. Cependant, la section de la CVG n'est pas circulaire mais ovale, et la vue échocardiographique mesure le petit diamètre de cet ovale, ce qui entraine une sous-estimation de 17% du diamètre réel; cette erreur est ensuite portée au carré dans le calcul de la surface (24% de difference) [4].
- VCCVG: vélocité maximale ou ITV de la CCVG mesuré au Doppler pulsé en vue long axe transgastrique à 0° ou 120° ; la fenêtre est positionnée 5 mm en amont de la valve aortique, au milieu du flux, en évitant de la placer dans la zone d'accélération pré-sténotique. Pour ce faire, on place le volume d'échantillonnage d'abord sous la valve, où l'image spectrale présente un large spectre de vélocités assez élevées; on le recule ensuite lentement en direction du VG jusqu'à ce qu'on obtienne une courbe à l'enveloppe fine et à la Vmax stable.
- VAo: vélocité maximale ou ITV à travers la valve aortique mesuré au Doppler continu en vue long axe transgastrique à 0° ou 120°. Alors que l'écho transthoracique (ETT) peut enregistrer la Vmax de la vena contracta en aval de la valve depuis le creux sus-sternal, l'ETO ne peut se positionner dans l'axe du flux aortique qu'en position transgastrique, soit en amont de la valve. L'axe Doppler doit donc traverser la sténose pour enregistrer la vena contracta, ce qui peut s'avérer très difficile lorsque la valve est sténosée, calcifiée et très remaniée. En général, la Vmax est sous-estimée par l'ETO.
- Comme les défauts d'axe Doppler sont approximativement les mêmes dans la CCVG et dans la sténose aortique, le rapport VCCVG / VAo présente l'intérêt d'éliminer cette source d'erreur. Normalement, ce rapport est ≥ 0.8. Lorsque la sténose aortique est serrée, il est ≤ 0.25, ce qui signifie que la Vmax à travers la valve est au moins 4 fois supérieure à celle dans la CCVG. Enregistrant toutes les vélocités dans l'axe des ultrasons, le Doppler continu affiche simultanément la Vmax à travers la valve et la Vmax à travers la chambre de chasse (technique dite de la "double enveloppe"). Toutefois, il est possible que la VCCVG mesurée de cette manière soit contaminée par la zone d'accélération présténotique et soit de ce fait artificiellement élevée [2].
Figure 11.163 : Application de l’équation de continuité au calcul de la surface d'une sténose aortique serrée. A: mesure du diamètre de la chambre de chasse en vue long-axe 120° (flèche verte). B: alignement du faisceau Doppler continu avec le flux aortique en vue transgastrique profonde 0°; la flèche verte pointe la valve aortique. C: enregistrement du flux Doppler continu selon la technique de la double enveloppe (affichage simultané de la Vmax à travers la valve aortique et à travers la CCVG sur la courbe du flux). La Vmax à travers la valve aortique est de 5 m/s (flèche jaune); la Vmax à travers la CCVG est de 0.8 m/s (flèche rouge); le diamètre de la CCVG est 2 cm. La surface de la valve aortique (S = (SCCVG•VCCVG)/VAo) est: (0.785 • 4 cm2 • 0.8 m/s) / 5 m/s = 0.5 cm2.
Le calcul de l'équation de continuité peut se faire de la même manière à différents endroits du flux sanguin (CCVD, artère pulmonaire, valve mitrale), mais toujours en prenant soin de placer l’axe Doppler au centre du flux pour éviter les variations de vélocités liées aux parois et aux courbures. La marge d'erreur est plus la grande au niveau de la valve mitrale, car son ouverture et son anneau ne sont pas circulaires; l'échantillonnage du Doppler pulsé doit se faire au niveau de l'anneau en diastole, là où se mesure la surface, et non dans le cône que forment les deux feuillets. La vélocité mesurée n'est donc pas la Vmax habituelle du flux mitral, qui est enregistrée au niveau de l'extrémité des feuillets. L'équation de continuité ne s'applique pas à une valve qui présente une régurgitation, car son volume systolique est additionné du volume régurgité qui doit être ré-éjecté, alors que l'autre localisation de la mesure ne subit pas cette altération. D'une manière générale, il est plus adéquat de remplacer la Vmax par l'intégrale des vélocités (ITV) dans le calcul. Bien que non-simultanées, les mesures de surface et de vélocité doivent se faire exactement au même endroit et au même temps du cycle cardiaque.
En cas d'insuffisance valvulaire, l'équation de continuité permet de calculer le volume de la régurgitation (VR), en prenant un autre lieu du flux comme référence et en faisant l'hypothèse que les surfaces valvulaires sont circulaires (ce qui est erroné pour la valve mitrale). Le volume systolique (VS) est le produit de la surface et de l'intégrale des vélocités (ITV) à cet endroit. La surface de l'orifice de régurgitation est le résultat de la division du volume régurgité par l'ITV du jet de l'insuffisance [3]. Exemple pour une insuffisance mitrale:
- VRV mitr = VSV mitr - VSCCVG = (SV mitr • ITVV mitr) - (SCCVG • ITVCCVG)
- VRV aort = VSCCVG - VSV mitr = (SCCVG • ITVCCVG) - (SV mitr • ITVV mitr)
- Fraction de régurgitation: FR = (VR / VS) • 100
- Orifice de régurgitation: OR = VRV mitr / ITVRég mitr
| Equation de continuité |
| Le flux, produit de la surface et de la vélocité (S • V), est identique tout au long d’un parcours: S1 • V1 = S2 • V2. Donc, le calcul d'une des surfaces devient: S2 = (S1 • V1) / V2. Pour une sténose aortique: SAo = (SCCVG • VCCVG) / VAo. L'utilisation de l'ITV est préférable à celle de la Vmax. Le calcul peut se faire de manière identique entre deux endroits du flux sanguin en continuité. En cas d'insuffisance valvulaire, l'équation de continuité permet de calculer le volume de la régurgitation en prenant un autre lieu du flux comme référence. |
© CHASSOT PG, BETTEX D. Avril 2019; dernière mise à jour, Mars 2020
Références
- BAX JJ, DELGADO V. Advanced imaging in valvular heart disease. Nat Rev Cardiol 2017; 14:209-23
- HUI S, MAHMOOD F, MATYAL R. Aortic valve area – Technical communication: continuity and Gorlin equations revisited. J Cardiothorac Vasc Anesth 2018; 32:2599-606
- MAHMOOD F, MATYAL R. Quantitative echocardiography. In: MATHEW JP, SWAMINATHAN M, AYOUB CM. Clinical manual and review of transesophageal echocardiography, 2nd edition. New York: McGraw-Hill 2010, 63-86
- O'BRIAN B, et al. Integration of 3D imaging data in the assessment of aortic stenosis: impact on classification of disease severity. Circ Cardiovasc Imaging 2011; 4:566-73
- QUINONES MA, OTTO CM, STODDARD M, et al. Recommendations for quantification of Doppler echocardiography: A report from the Doppler Quantification Task Force of the Nomenclature and Standards Committee of the American Society of Echocardiography. J Am Soc Echocardiogr 2002; 15:167-84
- ZOGHBI WA, ADAMS D, BONOW RO, et al. Recommendations for noninvasive evaluation of native valvular regurgitation: a report from the ASE developed in collaboration with the SCMR. J Am Soc Echocardiogr 2017; 30:303-71
25. Echocardiographie transoesophagienne 1ère partie
- 25.1 Introduction
- 25.2 Principes physiques de l'échocardiographie
- 25.3 Anatomie fonctionnelle
- 25.3.1 Technique et risques de l'ETO
- 25.3.2 Examen standard 2D
- 25.3.3 Examen des valves
- 25.3.4 Examen bidimensionnel des ventricules
- 25.3.5 Examen des oreillettes
- 25.3.6 Mode TM
- 25.3.7 Examen Doppler
- 25.3.8 Examen tridimensionnel (3D)
- 25.3.9 Mesures quantitatives
- 25.3.10 Examen rapide
- 25.3.11 Images artéfactuelles
- 25.3.12 Rapport d'examen
- 25.4 Mesures hémodynamiques
- 25.5 Fonction systolique du VG
- 25.6 Fonction diastolique du VG
- 25.7 Fonction ventriculaire droite
- 25.8 Fonction ventriculaire segmentaire
- 25.9 Insuffisance cardiaque
- 25.10 Place de l'ETO en clinique
- 25.11 ETO en chirurgie cardiaque
- 25.12 ETO en chirurgie non-cardiaque
- 25.13 Echocardiographie en soins intensifs
- 25.14 Echocardiographie au déchocage
- 25.15 Echocardiographie transthoracique
- 25.16 Conclusions





























